呼損率を求めたい

Posted bysiguniangPosted inalgorithmTags:, , ,

呼損率とは

通信回線の世界では呼損率(こそんりつ)という考え方がある。

ユーザーが電話サービスおよびISDNサービスを利用する時に，ビジーで利用できない率。呼がなんらかの理由（話中など）で拒絶されてサービスを受けることができない割合を指す。 http://itpro.nikkeibp.co.jp/word/page/10007943/

Erlang B formula を使うと呼損率を求めることができる。

wikipedia の Erlang (unit) に丁寧にまとめられているので、読めば一般の人が知りたいであろうことはわかる。

Erlang(単位)の定義

Erlang B formula には単位の Erlang が出てくるので、まずはこの定儀から。

λ:単位時間あたりの呼び出し件数
h:を1件あたりの処理時間

とした時に

E = λh

と定儀する。

例)
1時間あたり200回の呼び出し(200 call/hour)、1件あたり0.1時間(0.1 hour/call) かかるとすると

E = 200 * 0.1 = 20(erlang)

となる。

Erlang B formula の定義

早速覚えた単位 Erlang を使うと、ビジーだった時にリトライしない(loss system)という前提のもとで、次の式(Erlang B formula)で呼損率 P_b を求めることができる。

P_b = B(E,m) = \frac{\frac{E^m}{m!}} { \sum_{i=0}^m \frac{E^i}{i!}}

from math import factorial
def naive_erlanb_b(erlang, m):
    erlang *= 1.0
    numerator = erlang ** m / factorial(m)
    denominator = sum(erlang ** i / factorial(i) for i in range(m+1))
    return numerator / denominator

ここで m は並列処理数。

この式は、漸化式を使っても定義できることが知られている。

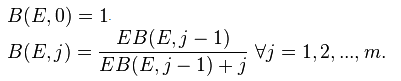
erlang_b_recursive

def erlang_b(erlang, m):
    erlang = float(erlang)
    if m == 0:
        return 1.0
    inv_b = 1.0 + (m / erlang)  / erlang_b(erlang, m-1)
    return 1.0 / inv_b

実務家向けには、数値的安定性から、逆数をとって計算するのが好ましい

\frac{1}{B(E,0)} = 1

\frac{1}{B(E,j)} = 1 + \frac{j}{E}\frac{1}{B(E,j - 1)} \ \forall{j} = 1,2,...,m.

実際に計算

では Erlang B Formula を使って、実際に計算する。

20 Erlang で m が 23 の場合、呼損率は 0.085

諸般の事情によりチャンネル数 m が 23 固定だとして(ISDNとか)

・ケース1
処理時間 h が同じまま、単位時間あたりの呼び出し件数λ が倍になったとする。

この時、Erlang は E = λh の形から当然倍の 40 になる。
すると、 呼損率 P_b = 0.4525 に跳ね上がる。

・ケース2
単位時間あたりの呼び出し件数λが同じまま、 処理時間 h が半分になったとする。
Erlang はさっきとは逆に半分の 10 になる。
すると、 呼損率 P_b = 0.00017 と激減する。

関連

Extended Erlang B

ビジーだった場合に、かけ直す場合

Erlang C Formula

ビジーだった場合に、キューに積まれる場合(コールセンターとか)

centum call second

http://en.wikipedia.org/wiki/Call-second
Erlang に似た単位として centum call second (CCS) というのもある。
1時間あたり100 call, 1 call あたり 1 秒を表す量なので、単位時間を秒に揃えると
1(CCS) = 100/60/60(call/second) * 1(second/call) = 1/36(Erlang) となる。

もっと数学よりの説明

Wiley Encyclopedia of Operations Research and Management Science : THE M/G/s/s QUEUE
http://www.wiley.com/WileyCDA/Section/id-397134.html

Leave a comment